大家有否想過,何解去旅行、公幹乘坐飛機時,當中的飛行路線必是曲線,而非直線呢?最近香港天文台 Facebook 就 post 了一條影片,為大家拆解兩個乘坐飛機冷知識,其中一個正是飛行路徑「必呈曲線」之謎,另一個就是有關飛行里數的真正解釋。原來飛行里數的計算,是跟乘坐航班編號的多寡有關的!
【相關報道】
【相關報道】
曲線飛行歸因地球形狀?
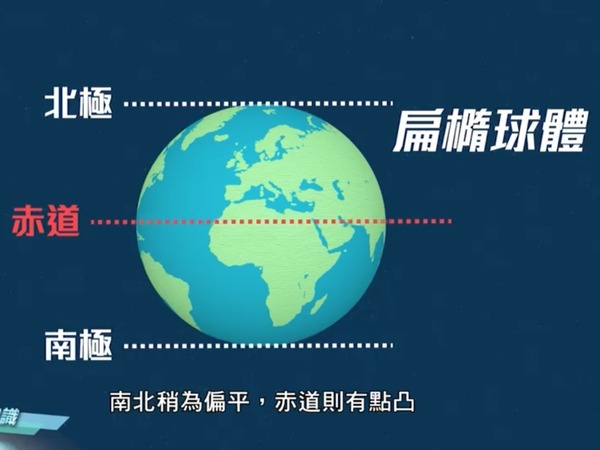
可能不少人乘坐飛機,看到飛行路線地圖是曲線而非直線時,就有「飛機兜路走」的聯想。其實事實並非如此。從香港天文台 Facebook 影片解釋可見,飛行路線路徑「必呈曲線」,是歸因於地球形狀是一個扁橢球體,南北稍為偏平,赤道有點突出,因此要量度由 A 地飛往 B 地的距離,並非像用直尺直線地度出兩地之間的長度,而是應將地球分為兩半,量度的兩點是需要穿過地心,從而得到最準確的數據。
大圓距離證「飛機沒有兜路走」
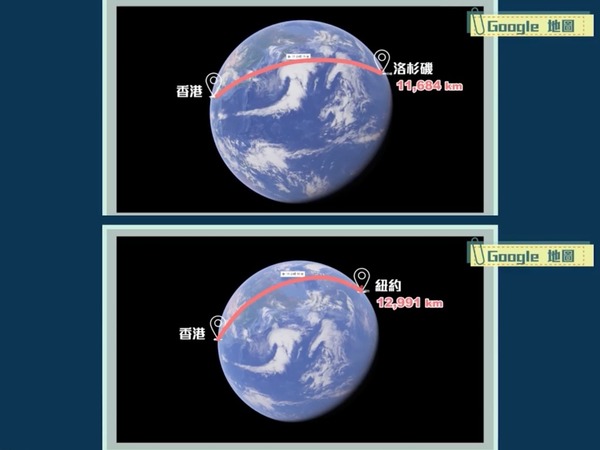
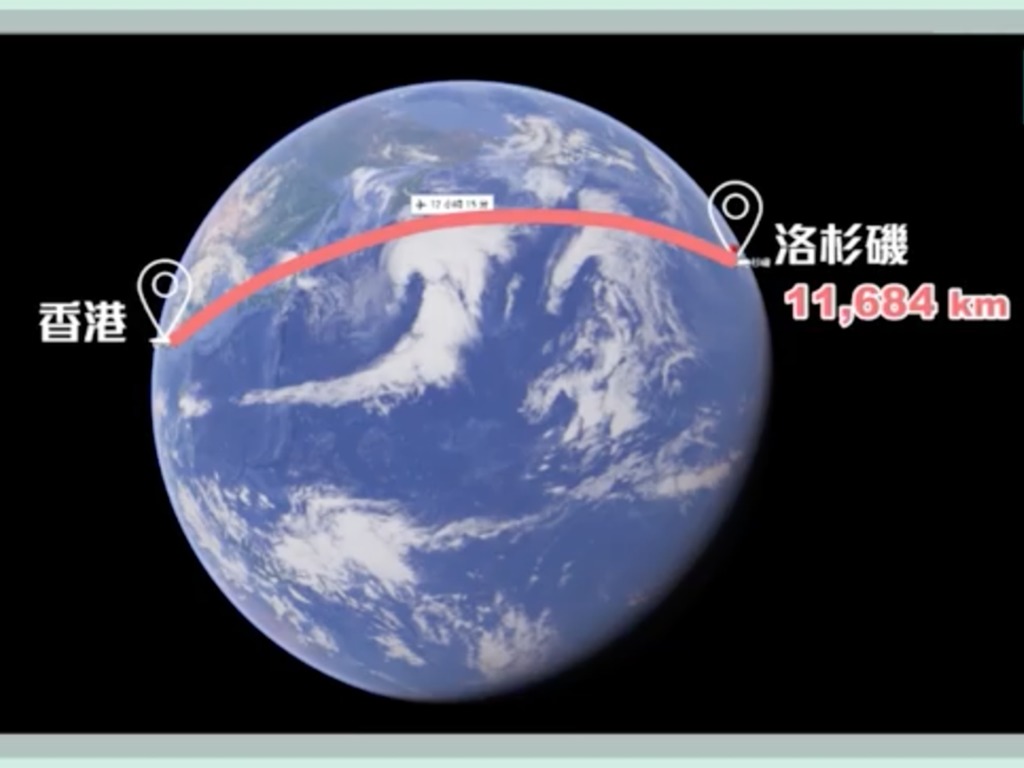
以上穿過地心,且將地球等分兩個相等扁橢球體的圓圈線,以量度由 A 地飛往 B 地的距離,稱為大圓距離(Great Circle Distance)。以這方法量度的話,例如香港至洛杉磯的最短飛行距離,就約為 11,684 公里,當中會先經韓國、日本,再到阿留申群島及太平洋而往下駛至洛杉磯;香港至紐約的最短飛行距離,就約為 12,991 公里,經西伯利亞及接近北極,然後在格陵蘭以西的加拿大東北再往下走至紐約。
正因如此,大圓距離已最接近最短飛行距離,加上飛行距離、時間的多少,也直接影響航空公司的營運,所以也證實「飛機兜路走」情況並不存在。當然,由 A 地飛往 B 地的最終飛行路徑,是會受天氣、地緣政治等因素影響,有否火山爆發、戰事、航空管制,又或者飛機航行時有否機會接觸較大劑量的太陽輻射等。
大圓距離 = 飛行里數數額多少
剛才提到大圓距離可視為由 A 地飛往 B 地之最短飛行距離,而大圓距離其實也反映大家平常儲飛行里數的數額。至於儲飛行里數的數額多少,原來跟大家乘坐的航班數量有關,而非因轉機次數影響。假如由 A 地,經 B 地轉飛到 C 地,是乘坐單一航班編號的飛機的話,當中也只會當作由 A 地直航至 C 地的單程航班數據計算;相反由 A 地,經 B 地轉飛到 C 地時,是乘坐兩個航班編號的飛機,那麼飛行里數的數額,就會同時計算由 A 地飛往 B 地、由 B 地飛往 C 地的兩程航班數據,致使當中所得的飛行里數也會較多。至於大家可以怎樣計算兩個城市之間距離,大概知道自己得到多少飛行里數,可以到 Great Circle Mapper 這個網站輸入機場代號,再按 Distance 鍵可見。
如在 Great Circle Mapper 這個網站輸入從香港(HKG)經溫哥華(YVR)飛往紐約(JFK)的路線為例,如乘坐單一航班編號的直航形式計算,所得之飛行里數約為 12,990 公里左右,乘坐兩個航班編號的飛機來計,所得之飛行里數則約為 10,2877(香港至溫哥華)加 3,941(溫哥華至紐約),等於 14,228 公里,兩者所得之飛行里數約相差 9.5%。
【相關報道】
【相關報道】
香港天文台 HKO Facebook Great Circle Mapper